Ir al contenido principal

LUGAR GEOMÉTRICO DE LINEAS RECTAS Y CURVAS



Un lugar geométrico es el conjunto de los puntos (x,y) que cumplen con una misma propiedad o condición geométrica, representada por una ecuación, esta puede ser representada en el plano cartesiano
.
Es aquel sistema de referencia formado por el corte perpendicular de dos rectas numéricas en un punto denominado origen del sistema. El corte de estas rectas determina en el plano cuatro regiones cada una de las cuales se va a denominar cuadrante. En el sistema de coordenadas rectangulares, el punto de intersección de las dos rectas se le llama origen del sistema.
Las rectas numéricas trazadas se van a denominar eje de abscisas y eje de las ordenadas.

Ubicación de un punto
Para ubicar un punto será necesario conocer los valores correspondientes a las proyecciones del punto considerado sobre cada uno de los ejes; así en el gráfico; las coordenadas que precisan a "P" son "x" e "y", a las cuales se va a denominar.
En el sistema de coordenadas Rectángulares, los valores de las abscisas a la derecha del origen son positivos. Y los valores del origen a la izquierda, serán negativos.
De la misma manera, en el eje Y, los valores del origen hacia arriba. Serán considerados positivos, y negativos del origen hacia abajo.
Ejemplo: Ubica los siguientes puntos en el sistema de ejes coordenados dado: A(3,2), B(-3,2), C(3,-2), D(-3,-2), E(1,1), F(-1,2), G(0,5) y H(3,0).
Rendered by QuickLaTeX.com
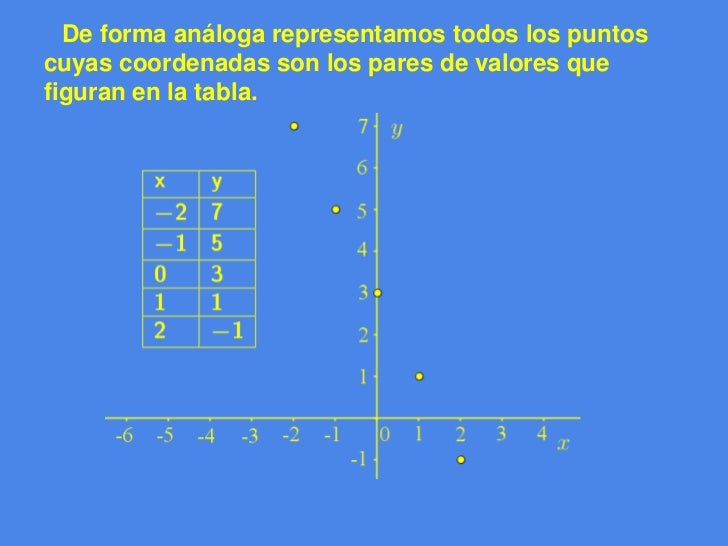
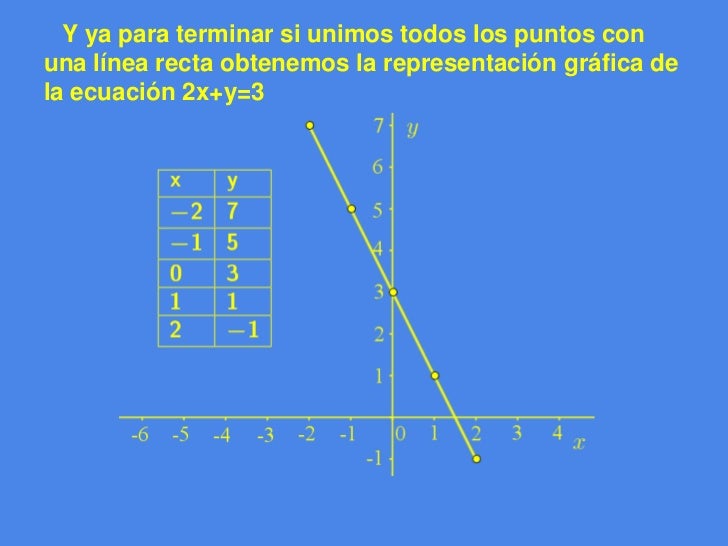
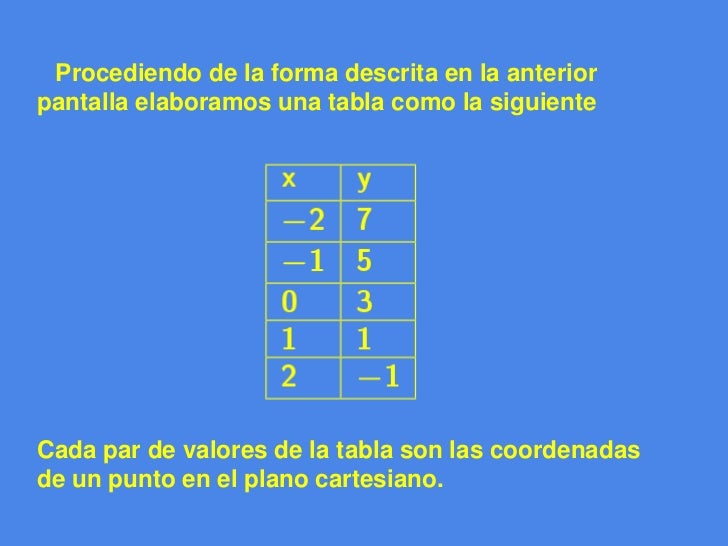
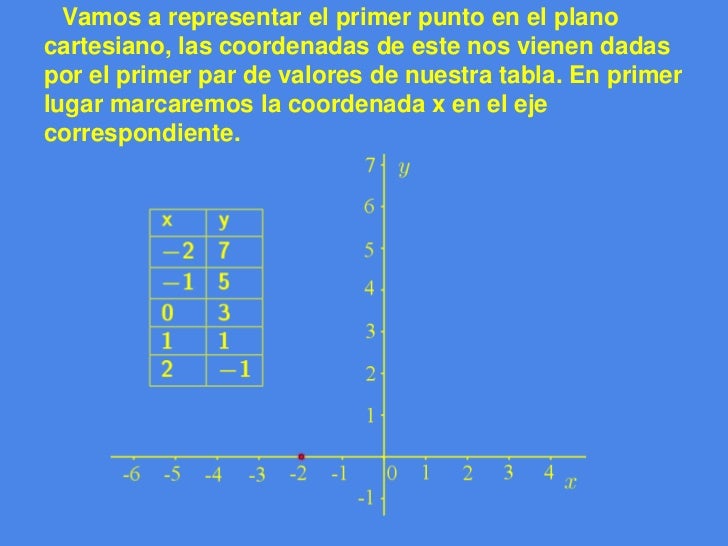
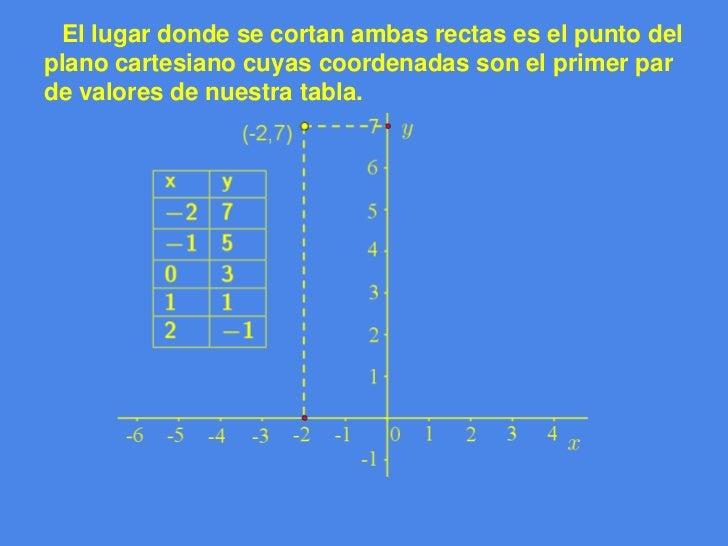
REPRESENTAR UN LUGAR GEOMÉTRICO 
Ejemplo: 
2x + y = 3 
1º Vamos a elaborar una tabla de valores para ellodespejamos la y. 2x+y=3 ...
Procediendo de la forma descrita en la anteriorpantalla elaboramos una tabla como la siguienteCada par de valores de la ta...
Vamos a representar el primer punto en el planocartesiano, las coordenadas de este nos vienen dadaspor el primer par de va...El lugar donde se cortan ambas rectas es el punto delplano cartesiano cuyas coordenadas son el primer parde valores de nue...
De forma análoga representamos todos los puntoscuyas coordenadas son los pares de valores quefiguran en la tabla.
Y ya para terminar si unimos todos los puntos conuna línea recta obtenemos la representación gráfica dela ecuación 2x+y=3
Este video también te puede ayudar:  
https://www.youtube.com/watch?reload=9&v=954jkmsM_78

Etiquetas:

Comentarios

Publicar un comentario

Entradas más populares de este blog

DISTANCIA DE UN PUNTO A UNA RECTA

Dado un punto P(x 1 ,y 1 ) y la recta L (Ax + By + C=0), la distancia dirigida (es decir, hacia un solo sentido) de P a L se determina con la siguiente ecuación: Se dirá que la distancia es positiva cuando el punto P y el origen están del mismo lado de la recta. De no ser así, la distancia será negativa.         Si se quiere obtener la distancia absoluta (sin importar el sentido) se usa la siguiente ecuación: Ejemplo: Determina la distancia dirigida del punto P(7,-1) a la recta L(4x-5y-13=0). Se sustituyen los valores en la ecuación que calcula la distancia del punto a la recta, cuidando el signo en la parte de abajo de dicha fórmula:  
Publicar un comentario
Leer más

PUNTO-PENDIENTE

Forma punto - pendiente de la ecuación de una recta. Una de las primeras formas de representar la ecuación de una recta es la llamada punto - pendiente, como su nombre lo indica, los datos que se tienen son un punto y una pendiente. Sea A(x1, y1) el punto dado y m la pendiente dada de la recta, entonces si consideramos otro punto cualquiera B(x, y), que forme parte de dicha recta, por la definición de pendiente se tiene que:  Agrupando términos nos queda:
Publicar un comentario
Leer más

RECTAS PARALELAS Y PERPENDICULARES

Paralelismo . Dos rectas son paralelas si la distancia entre ellas es constante y por lo tanto, por mucho que se propaguen nunca se cruzan. En función de sus pendientes, dos rectas serán paralelas si sus pendientes son iguales. Por lo tanto:                   m1= m2                       Condición de paralelismo De la cual: m1 = pendiente de la primer recta. m2 = pendiente de la segunda recta. Perpendicularidad . Dos rectas son perpendiculares si al cruzarse forman ángulos de 90º. En función de sus pendientes, dos rectas serán perpendiculares si el producto de sus pendientes es igual a -1, Por lo tanto:                      m1*m2 = -1                     Condición de perpendicularidad. De la cual: m1 ...
Publicar un comentario
Leer más