Ir al contenido principal

DIVISIÓN DE UN SEGMENTO ENTRE UNA RAZÓN DADA

La razón es el cociente, una comparación entre dos tramos de un segmento. 

En el siguiente ejemplo, se muestra que en el segmento AB, P, es un punto ubicado dentro de la recta. Para obtener la razón de esta recta, primer debemos comprender que es distinto si tomamos la razón de ARRIBA a ABAJO, que al revés.  El sentido de donde tomemos la razón es importante, generalmente, tomamos el punto más abajo al que se encuentra en la parte de arriba. El sentido importa.
Imagen
La razón es una comparación entre dos extremos de una recta, entonces, la fórmula para obtener una razón, (que a partir de ahora representaremos con la letra r), será r= AP/PB.
 La fórmula para calcular valor en "x" y valor en "y" del punto P es la siguiente.
Resultado de imagen para division de un segmento en una razon dada formula
Donde r será la razón 
Ejercicio: 
a) En un segmento AB, donde A tiene coordenadas (6,-3) y B(1,6). Hallar coordenadas de del punto P, si la razón es de 4.
​
Imagen
RESOLUCIÓN:
​Tenemos que considerar el sentido de la razón, ya que si lo hacemos al revés, tendríamos una razón de 1/4.
Utilizando la fórmula de la coordenada de x:
x= (x1+rx2)/(1+r)
Sustituyendo valores, quedaríax=(6+4*1)/(1+4)
x=10/5            x=2

Utilizando la fórmula de la coordenada de y:
y= (y1+ry2)/(1+r)
Sustituyendo valores, quedaríay=(-3+4*6)/(1+4)
y=21/5            y=4.25
Así obtenemos las coordenadas de P (2,4.25). y a continuación se procede a representar : 
Imagen

Este video te puede ayudar si aun no has comprendido:

Etiquetas:

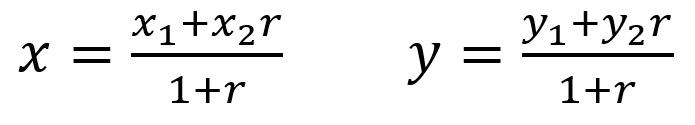
Comentarios

Publicar un comentario

Entradas más populares de este blog

DISTANCIA DE UN PUNTO A UNA RECTA

Dado un punto P(x 1 ,y 1 ) y la recta L (Ax + By + C=0), la distancia dirigida (es decir, hacia un solo sentido) de P a L se determina con la siguiente ecuación: Se dirá que la distancia es positiva cuando el punto P y el origen están del mismo lado de la recta. De no ser así, la distancia será negativa.         Si se quiere obtener la distancia absoluta (sin importar el sentido) se usa la siguiente ecuación: Ejemplo: Determina la distancia dirigida del punto P(7,-1) a la recta L(4x-5y-13=0). Se sustituyen los valores en la ecuación que calcula la distancia del punto a la recta, cuidando el signo en la parte de abajo de dicha fórmula:  
Publicar un comentario
Leer más

PUNTO-PENDIENTE

Forma punto - pendiente de la ecuación de una recta. Una de las primeras formas de representar la ecuación de una recta es la llamada punto - pendiente, como su nombre lo indica, los datos que se tienen son un punto y una pendiente. Sea A(x1, y1) el punto dado y m la pendiente dada de la recta, entonces si consideramos otro punto cualquiera B(x, y), que forme parte de dicha recta, por la definición de pendiente se tiene que:  Agrupando términos nos queda:
Publicar un comentario
Leer más

RECTAS PARALELAS Y PERPENDICULARES

Paralelismo . Dos rectas son paralelas si la distancia entre ellas es constante y por lo tanto, por mucho que se propaguen nunca se cruzan. En función de sus pendientes, dos rectas serán paralelas si sus pendientes son iguales. Por lo tanto:                   m1= m2                       Condición de paralelismo De la cual: m1 = pendiente de la primer recta. m2 = pendiente de la segunda recta. Perpendicularidad . Dos rectas son perpendiculares si al cruzarse forman ángulos de 90º. En función de sus pendientes, dos rectas serán perpendiculares si el producto de sus pendientes es igual a -1, Por lo tanto:                      m1*m2 = -1                     Condición de perpendicularidad. De la cual: m1 ...
Publicar un comentario
Leer más